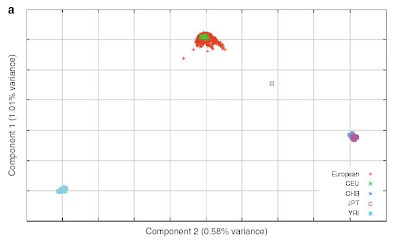
6.1.1. The inverse cubic law distribution of stock price fluctuations:
The tail distribution of short-term (15 s to a few days) returns has been analyzed in a series of studies on data sets, with a few thousands of data points (Jansen & de Vries 1991, Lux 1996, Mandelbrot 1963), then with an ever increasing number of data points: Mantegna & Stanley (1995) used 2 million data points, whereas Gopikrishnan et al. (1999) used over 200 million data points. Gopikrishnan et al. (1999) established a strong case for a inverse cubic PL of stock market returns.
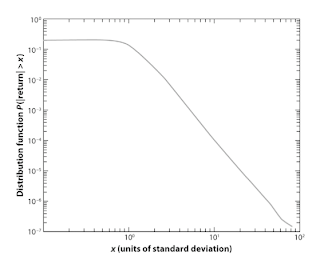
...Such a fat-tail PL yields a large number of tail events. Considering that the typical standard daily deviation of a stock is approximately 2%, a 10–standard deviations event is a day in which the stock price moves by at least 20%. From daily experience, the reader can see that those moves are not rare at all: Essentially every week a 10–standard deviations event occurs for one of the (few thousand) stocks in the market.28 The cubic law quantifies that notion and states that a 10–standard deviations event and a 20–standard deviations event are 5^3 = 125 and 10^3 = 1000 times less likely, respectively, than a 2–standard deviations event.
The figure below shows the probability distribution of 15 minute returns on 1000 large company stocks from data taken in 1994-1995. (Click for larger version.)
Here is a figure showing the famous power law scaling of metabolic rate with body mass in animals (click for larger version):